30 Contoh Soal Matematika SMP Lengkap dengan Jawaban & Pembahasan

Berikut 30 contoh soal Matematika SMP kurikulum Merdeka untuk kelas 7, 8, dan 9 lengkap dengan jawaban serta pembahasan mudah dipahami.

Belajar mandiri di rumah bisa sangat bermanfaat, salah satunya melatih kemampuan mengingat dan memahami sampai bisa mengerjakannya “di luar kepala”. Apalagi mata pelajaran Matematika yang tidak cukup dikerjakan hanya di ruang kelas saja.

Supaya makin jago, berikut 30 contoh soal Matematika SMP kurikulum Merdeka dan cara mengerjakannya dari semua jenjang kelas yang bisa digunakan untuk berlatih sendiri di rumah. Jangan lupa kerjakan di tempat dan kondisi yang kondusif supaya bisa fokus. Semoga soal-soal ini membantu, ya!

10 Contoh Soal MTK Kelas 7 SMP

Melansir detikEdu, berikut contoh soal Matematika yang bisa dikerjakan untuk murid kelas 7 SMP. Selamat berlatih!

1. Di antara bilangan berikut yang merupakan bilangan yang terkecil adalah….

A. 6

B. 1

C. 4

D. -1

Jawaban: D

Pembahasan: Nilai bilangan bulat semakin ke kiri semakin kecil. Jika diurutkan sesuai dengan garis bilangan, maka urutannya -1, 1, 4, 6. Sebab itu, jawabannya adalah -1.

2. Hasil penjumlahan (-4) + (-3) adalah…

A. 7

B. -7

C. 3

D. -3

Jawaban: B

Pembahasan: Jika dua bilangan negatif dijumlahkan, hasilnya tetap negatif dengan kedua bilangan dijumlahkan. Jadi, hasil (-4) + (-3) adalah -7.

3. Hasil penjumlahan dari (25 x 4) x 13 adalah….

A. 13

B. 130

C. 1.300

D. 13.000

Jawaban: C

Pembahasan:

= (25 x 4) x 13

= 100 x 13

= 1.300

4. Bilangan bulat yang berada di antara -3 dan 3 adalah….

A. -3, -2, -1, 0, 1, 2, 3

B. -3, -2, -1, 0, 1, 2

C. -2, -1, 0, 1, 2, 3

D. -2, -1, 0, 1, 2

Jawaban: D

Pembahasan: Jika diurutkan dengan garis bilangan, maka urutannya -3, -2, -1, 0, 1, 2, 3

5. Setiap hari, Catur menabung sebesar Rp500. Jika hari ini tabungan Catur Rp12.500 maka besar tabungan Catur tiga belas hari yang akan datang adalah….

A. Rp19.000

B. Rp18.500

C. Rp13.000

D. Rp6.000

Jawaban: A

Pembahasan: Catur menabung Rp500 per hari, maka tabungan 13 hari kemudian adalah Rp500 x 13 = Rp6.500 ditambah dengan tabungan yang sudah ada maka Rp12.500 + Rp6.500 = Rp19.000 jawabannya.

6. Nilai dari (-6)3 adalah….

A. -216

B. -12

C. 64

D. 216

Jawaban: A

Pembahasan: (-) x (-) = (+) x (-) = (-) maka (-6) x (-6) = 36 x (-6) = -216.

7. Diketahui A = {2,3,4} dan B = {1,3}. Maka A ⋃ B adalah….

A. {3}

B. {1, 2, 3, 4}

C. {1, 3}

D. {2, 4}

Jawaban: A

Pembahasan: Simbol ⋃ berarti gabungan semua anggota himpunan, sehingga A ⋃ B adalah {1, 2, 3, 4}.

8. Penyelesaian dari m + 3 = 13 adalah….

A. 6

B. 7

C. 8

D. 10

Jawaban: D

Pembahasan:

m + 3 = 13

m = 13 – 3

m = 10

9. Diketahui 2x + 5 = 13, nilai x (untuk x bilangan asli) adalah….

A. 4

B. 5

C. 6

D. 8

Jawaban: A

Pembahasan:

2x + 5 = 13

2x = 13 – 5

2x = 8

x = 8 : 2

x = 4

10. Bentuk pecahan 30% adalah….

A. 1/30

B. ⅓

C. 3/10

D. 3/100

Jawaban: C

Pembahasan: 30% = 30/100 disederhanakan menjadi 3/10.

Foto: Max Fischer/Pexels

10 Contoh Soal MTK Kelas 8 SMP

Berikut 10 contoh soal MTK kelas 8 SMP yang bisa dikerjakan di rumah seperti dilansir dari detikEdu. Kerjakan dulu sebelum melihat jawabannya, ya!

1. Sederhanakan bentuk perpangkatan berikut ke dalam bentuk baku! 83 x 25 x 106 = ….

A. 1,6384 x 103

B. 1,6384 x 102

C. 1,6384 x 105

D. 1,6384 x 106

Jawaban: B

Pembahasan:

83 = (23)3 = 23×3 = 29

29 x 25 = 29+5 = 214

214 x 106

= 16.384 x 106

2. Jika a = 32 dan b = 243, maka hasil operasi dalam bentuk perpangkatan yang paling sederhana dari 2a x 3b, yaitu….

A. 2a x 3b = 23 x 33

B. 2a x 3b = 24 x 34

C. 2a x 3b = 26 x 36

D. 2a x 3b = 23 x 36

Jawaban: C

Pembahasan:

= 2a x 3b = 2(32) x 3(243)

= 64 x 729 lalu ubah bentuk menjadi perpangkatan menjadi 26 x 36

Maka 2a x 3b = 26 x 36

3. Diketahui kelompok tiga bilangan berikut:

(i) 3, 4, 5

(ii) 5, 13, 15

(iii) 7, 24, 25

(iv) 20, 21, 29

Kelompok bilangan di atas yang merupakan tripel Pythagoras adalah….

A. (i), (ii), dan (iii)

B. (i) dan (iii)

C. (ii) dan (iii)

D. (i), (iii), dan (iv)

Jawaban: D

4. Suatu segitiga siku-siku memiliki panjang hipotenusa 17 cm dan panjang salah satu sisi tegaknya adalah 15 cm. Panjang sisi tegak lainnya adalah….

A. 6 cm

B. 8 cm

C. 12 cm

D. 16 cm

Jawaban: B

Pembahasan:

Ingat tripel Pythagoras (8, 15, 17) atau pahami rumus berikut.

c2 = a2 + b2 dengan c = hipotenusa (sisi miring)

172 = 152 + b2

289 = 225 + b2

b2 = 289 – 225

b2 = 64 = 8 cm

5. Pada segitiga sama sisi ABC, diketahui panjang sisi 8 cm. Tinggi segitiga tersebut adalah….

A. 42

B. 43

C. 32

D. 33

Jawaban: B

Pembahasan:

t = s2 – s22

t = 82 – 822

t = 64 – 16

t = 48

t = 16 x 3 = 43

6. Panjang sisi siku-siku suatu segitiga siku-siku berturut-turut 4a cm dan 3a cm. Jika panjang sisi hipotenusanya adalah 70 cm, keliling segitiga tersebut adalah….

A. 136 cm

B. 144 cm

C. 168 cm

D. 192 cm

Jawaban: C

Pembahasan:

Cari nilai a

(hipotenusa)2 = (sisi 1)2 + (sisi 2)2

702 = (4a)2 + (3a)2

4900 = 16a2 + 9a2

4900 = 25a2

a2 = 490025 = 196

a2 = 196 = 14

Cari panjang sisi

4a = 4 × 14 = 56 cm

3a = 3 × 14 = 42 cm

Hipotenusa = 70 cm

Hitung keliling

Keliling = 56 + 42 + 70 = 168 cm

7. Andi, Budi, Cahya, Dedi berada pada masing-masing pojok sebuah lapangan berbentuk persegi panjang yang berukuran 80 m x 60 m. Jarak terjauh di antara mereka adalah….

A. 60 m

B. 80 m

C. 90 m

D. 100 m

Jawaban: D

Pembahasan:

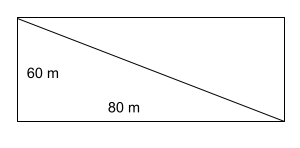
Jarak terjauh di antara mereka adalah dua sudut diagonal yang berseberangan, sehingga soal ini bisa dipecahkan menggunakan teorema Pythagoras:

(hipotenusa)2 = (sisi 1)2 + (sisi 2)2

(hipotenusa)2 = 802 + 602

(hipotenusa)2 = 6400 + 3600

(hipotenusa)2 = 10.000

(hipotenusa)2 = 100 m

8. Penyelesaian dari 8x − (5x − 4) > −5 adalah….

A. x > 3

B. x < 3

C. x > -3

D. x < -3

Jawaban: C

Pembahasan:

8x − (5x − 4) > -5

8x − 5x + 4 > -5

3x + 4 > −5

3x > −5 − 4

3x > -9

x > -9/3

x > -3

9. Ayah Dhoni seorang marketing dari suatu showroom mobil yang dibayar setiap bulan berdasarkan mobil yang terjual setiap bulannya. Terdapat aturan showroom bahwa untuk menjadi atasan, gaji rata-rata tiap bulan setidaknya Rp2.000.000 per 6 bulan. Sedangkan, gaji Ayah Dhoni selama 5 bulan pertama adalah Rp1.800.000, Rp2.300.000, Rp1.500.000, Rp2.000.000, dan Rp2.500.000. Gaji yang harus diterima Ayah Dhoni di bulan keenam untuk menjadi atasan adalah….

A. Rp1.900.000

B. Rp2.000.000

C. Rp2.100.000

D. Rp2.200.000

Jawaban: A

Pembahasan:

Hitung jumlah gaji 5 bulan pertama, yaitu 1.800.000 + 2.300.000 + 1.500.000 + 2.000.000 + 2.500.000 = Rp10.100.000

Kemudian hitung rata-rata 6 bulan:

jumlah gaji 5 bulan + gaji ke-66 2.000.000

10.100.000 + x6 2.000.000

10.100.000 + x 2.000.000 x 6

10.100.000 + x 12.000.000

x 12.000.000 – 10.100.000

x 1.900.000

10. Sederhanakan bentuk berikut 3x + 5x – 7!

A. 3x – 7

B. 5x – 7

C. 6x – 7

D. 8x – 7

Jawaban: D

Pembahasan:

3x + 5x – 7

= 8x – 7

Foto: August de Richelieu/Pexels

10 Contoh Soal MTK Kelas 9 SMP

Semakin tinggi kelasnya, materinya juga semakin susah. Tetapi dengan latihan soal yang cukup seseorang pasti bisa menguasainya. Berikut contoh soal MTK kelas 9 SMP dilansir dari detikEdu.

1. Hasil dari 24 x 3 + 15 : 3/4 – 7 adalah….

A. 109

B. 99

C. 85

D. 45

Jawaban: C

Pembahasan:

(24 x 3) + (15 : 3/4) – 7 = …

72 + (15/1 x 4/2) – 7 = …

72 + 20 – 7 = 85

2. Seorang pemborong memperkirakan dapat menyelesaikan proyek selama 60 hari dengan 20 pekerja. Setelah dikerjakan selama 15 hari, proyek terhenti selama 9 hari. Agar proyek selesai tepat waktu, maka diperlukan tambahan pekerja sebanyak….

A. 5 orang

B. 10 orang

C. 15 orang

D. 25 orang

Jawaban: A

Pembahasan:

60 hari = 20 pekerja

15 hari = 20 pekerja

Pekerja = (60 x 20) – (15 x 20)/(60 – 15 – 9)

Pekerja = (1200 – 300)/36

Pekerja = 900/36

Pekerja = 25

Sehingga pekerja tambahan yang dibutuhkan adalah 25 – 20 = 5 orang.

3. Hasil dari 3^-5 x 3^7/3^4 adalah….

A. -1/27

B. -1/9

C. 1/27

D. 1/9

Jawaban: D

Pembahasan:

3^-5 x 3^7/3^4

= (1/243 x 2187)/81

= 9/81

= 1/9

4. Andi menyimpan uang di koperasi sebesar Rp1.500.000. Koperasi memberi bunga tabungan sebesar 10% tiap tahun. Jika Andi menabung selama 8 bulan, maka jumlah bunga tabungan yang diterima Andi adalah….

A. Rp125.000

B. Rp120.000

C. Rp100.000

D. Rp90.000

Jawaban: C

Pembahasan:

Ibaratkan bila jumlah tabungan yang diterima Andi adalah X, maka X adalah:

X = Rp1.5000.00 x (8/12) x 10%

X = Rp1.5000.00 x (8/12) x 10/100

X = Rp1.5000.00 x (2/3) x 10

X = Rp5.000 x 2 x 10

X = Rp100.000

5. Dua suku berikutnya dari barisan 3, 4, 6, 9, …, … adalah ….

A. 13, 18

B. 13, 17

C. 12, 26

D. 12, 15

Jawaban: A

Pembahasan:

Perhatikan pola dari baris bilangan berikut.

3, 4, 6, 9

-1, +2, +3

Pola tersebut memperlihatkan bilangan ditambah bilangan asli berurutan, maka suku selanjutnya, yakni:

9 + 4 = 13

13 + 5 = 18

6. Sebuah taman kanak-kanak memiliki 40 siswa, diketahui bahwa 30 siswa gemar mewarnai, 20 siswa gemar menggambar, dan 17 siswa gemar keduanya. Maka banyak siswa yang tidak gemar keduanya adalah … siswa.

A. 3

B. 5

C. 7

D. 11

Jawaban: C

Pembahasan:

Jumlah siswa + siswa gemar keduanya = siswa gemar mewarnai + gemar menggambar + tidak gemar keduanya

40 + 17 = 30 + 20 + x

57 = 50 + x

x = 57 – 50

x = 7 siswa

7. Gradien garis yang tegak lurus dengan garis 3x + 2y – 5 = 0 adalah….

A. 3/2

B. ⅔

C. -⅔

D. -3/2

Jawaban: B

Pembahasan:

3x + 2y – 5 = 0

2y = -3x + 5

y = (-3x + 5)/2

y = -3/2x + 5/2

Maka gradien m1 adalah -3/2

Jika saling tegak lurus, maka:

m1 x m2 = -1

-3/2 x m2 = -1

m2 = -1 x -⅔

m2 = ⅔

8. Sebuah tongkat yang tingginya 1,5 m mempunyai bayangan 1 m. Jika pada saat yang sama bayangan sebuah tiang bendera adalah 2,5 m maka tinggi tiang bendera tersebut adalah….

A. 3,75 m

B. 2,75 m

C. 2,5 m

D. 2 m

Jawaban: A

Pembahasan:

Gunakan persamaan berikut.

1,5/1 = tinggi tiang bendera/2,5

x = 1,5 x 2,5/1

x = 3,75 m

9. Panjang diagonal sisi sebuah kubus adalah 8 cm. Maka luas permukaan kubus tersebut adalah … cm2.

A. 512

B. 384

C. 192

D. 96

Jawaban: C

Pembahasan:

Diagonal sisi = s2

8 = s2

8/2 = s

4/2 = s

Luas = 6 x s2

= 6 x (4/2)2

= 6 x 32

= 192 cm2

10. Sebuah tanah berbentuk setengah lingkaran dengan diameter 42 m. Di sekeliling tanah tersebut akan ditanami pohon kelapa dengan jarak antar pohon 3 m. Banyak pohon kelapa yang dibutuhkan adalah….

A. 36

B. 46

C. 56

D. 66

Jawaban: A

Pembahasan:

Keliling tanah = jumlah semua sisi

Keliling tanah:

1/2 x keliling lingkaran + diameter lingkaran

1/2 x 2πr + 2r

= πr + 2r

= 22/7 x 21 + 2 x 21

= 66 + 42

= 108 m

Banyak pohon kelapa: 108/3 = 36 buah

Itu dia kumpulan contoh soal Matematika SMP dengan kurikulum Merdeka. Semoga bisa meningkatkan kemampuan berhitungnya, ya!

Penulis: Retno Raminne Nurhaliza Pitoyo

Cover: Black ice/Pexels

Mommies Daily